跨导
栅源电压变化引起的漏极电流变化,定义为
线性区
饱和区
体效应
由于衬底B比源S的电位更负时,而导致的阈值电压的变化
为 体效应系数 0.3 ~ 0.4
引入概念 衬底跨导
衬底跨导
的变化导致的 的变化
体效应可以理解为衬底电压降低或栅极电压加高(只是理解上,而不是指实际的栅极加高)的的变化

注意
PMOS是可以不存在体效应的,因为PMOS独占N阱,PMOS的B和S是可以接在一起的,也就不存在B和S间的电位差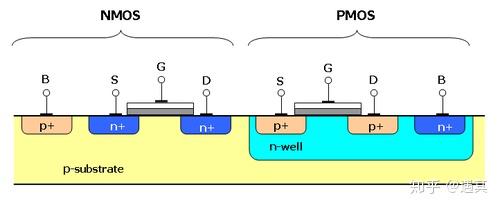
沟长调制效应
过大,产生了沟道夹断之后导致的沟道长度的变化,因为即使发生夹断,当V_{DS}增加时,仍然会增加
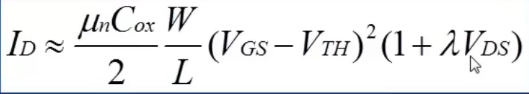
其中上式就是饱和区 考虑了沟长调制效应之后的式子, 就是沟长调制系数
小信号分析
不考虑任何二阶效应时
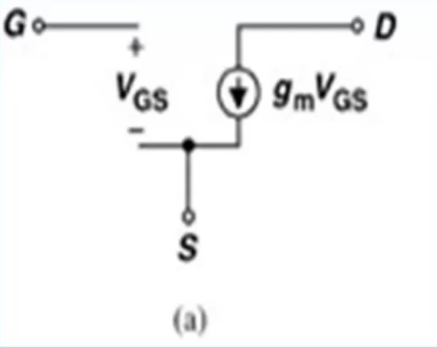
下图为工作在饱和区的MOS管时,引入小信号,这里可以当做 压控流源,受电压控制的电流源
为控制的电压, 为电流源
考虑沟长调制效应
下图为考虑沟长调制效应之后的模型,添加一个控制的电流源,系数为 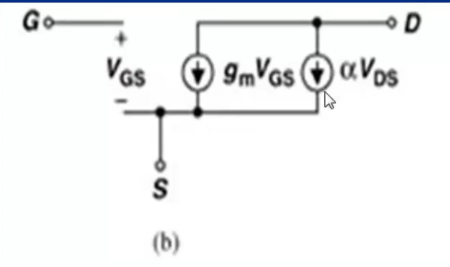
而这个模型中,可以看做,因此可以等效为电阻 ,即MOS输出阻抗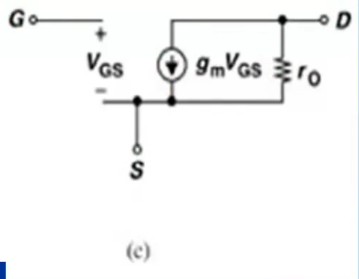
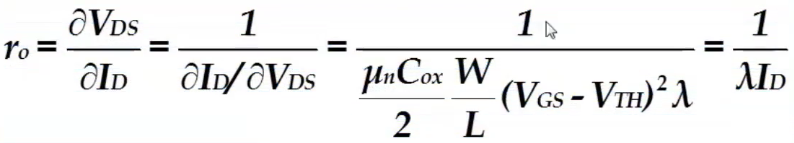
考虑体效应
下图为再考虑体效应的模型,为添加一个受控制的电流源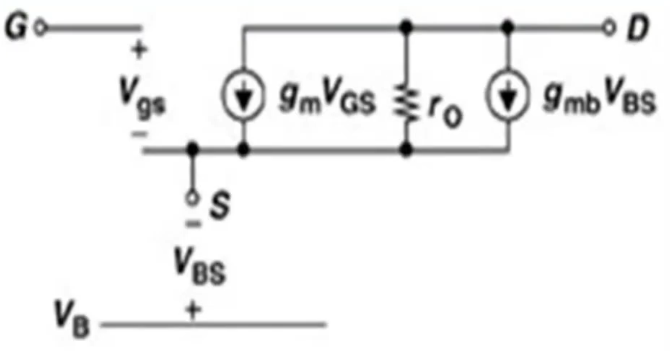
注意 虽然写作 但实际上 B<S 即, 为负
作者:odjvnrij 创建时间:2024-10-14 17:18
最后编辑:odjvnrij 更新时间:2024-11-28 16:14
最后编辑:odjvnrij 更新时间:2024-11-28 16:14
